HTML Preview Abacus telraam instructie page number 1.
De werking van ‘De Abacus’
Pagina 1 van 15
I. INLEIDING
Graag vertellen we u wat meer over de abacus.
De oudste gevonden rekenhulpmiddelen dateren van zo’n zesduizend jaar vóór Christus. De Romeinen gebruikten
kleivormpjes of ‘tokens’, in de vorm van kegeltjes, bollen, piramidetjes en cilinders om getallen mee uit te drukken.
Ongeveer duizend jaar vóór Christus hebben de Chinezen deze kleivormpjes vervangen door kralen met een gaatje
erin geboord. De kralen reeg men op rietstengels of koorden en later op houten of metalen pennen. Men stopte de
houten of metalen pennen in een houten bakje en men had een telraam … abacus.
De abacus wordt al duizenden jaren gebruikt in China en Japan. Zelfs tot de dag van vandaag! De abacus wordt
beschouwd als de voorloper van de computer (to compute = tellen). In 1946 werd er een rekenwedstrijd gehouden
tussen een Japanner met abacus en een computer. De Japanner won overtuigend. Nog altijd kunnen ervaren
abacusrekenaars veel berekeningen sneller uitvoeren dan rekenaars die gebruikmaken van een rekenmachine.
De kennis van het telraam kan in korte tijd geleerd worden, het gebruik ervan is een kunst. Men moet veel oefenen;
zekerheid krijgt men door het voortdurend gebruik, niet door leren.
De veelzijdigheid van de abacus is de grondslag voor de naam van ons kantoor. Een veelzijdigheid en diepgang, welke
aan geen enkel ander voorwerp kunnen worden toegedicht.
De Chinese abacus
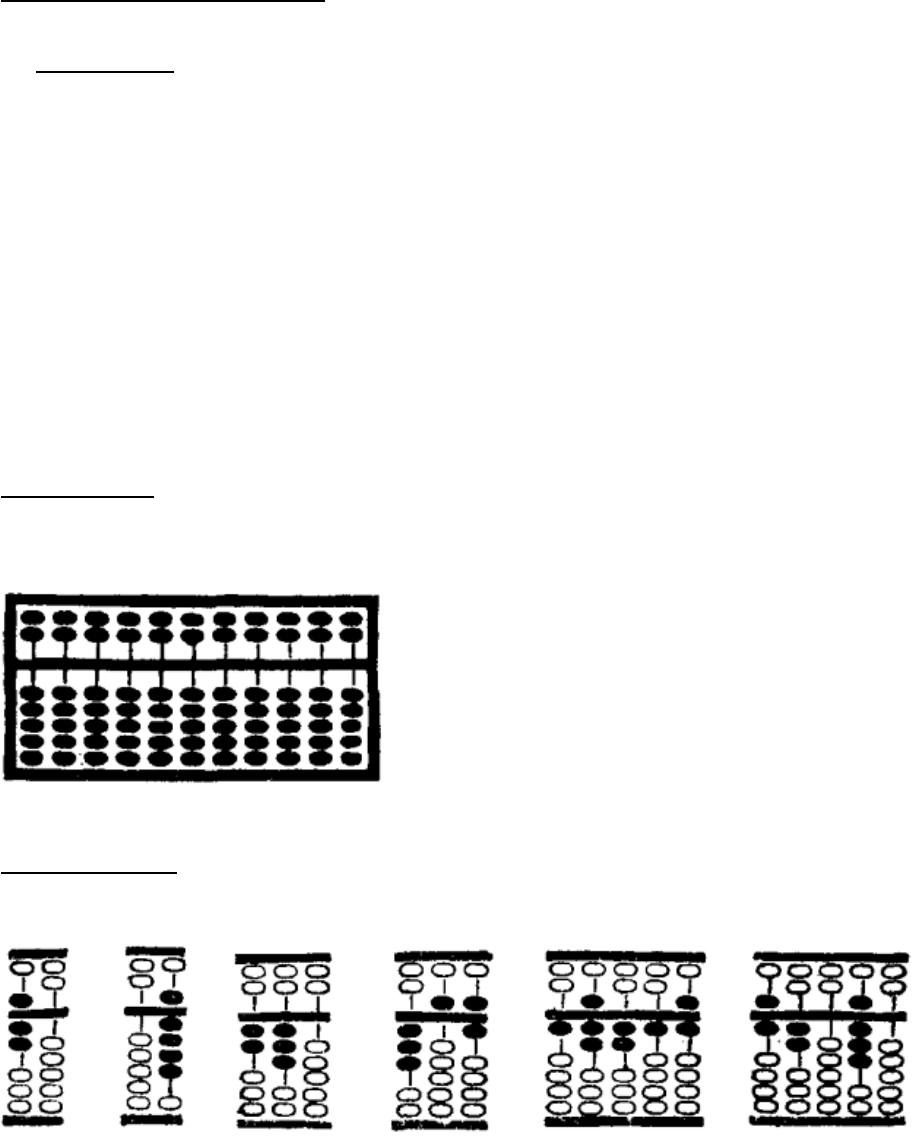
De abacus bestaat uit een houten raam, houten kralen en rijen. Het raam is door een dwarshout in twee delen gedeeld.
De gewone abacus heeft 9, 11 of 13 rijen. Het bovenste deel heeft telkens 2 kralen; de ‘bovenkralen’. Het onderste
deel heeft telkens 5 kralen; de ‘onderkralen’. De hoogste kraal wordt "bovenste kraal" genoemd.
Figuur 1
Waarde van de kralen
Iedere bovenkraal is gelijk aan 5 onderkralen van dezelfde rij. Iedere onderkraal is gelijk aan 10 van de aansluitende
rechtse rij. De volgende afbeeldingen stellen derhalve resp. voor: 7, 9, 23, 356, 17.216 en 6.208.
Figuur 2
Een nul wordt door een opening vastgesteld. Er kunnen moeilijkheden ontstaan als op deze nul geen cijfers volgen.
Dus kan de eerste afbeelding van figuur 2 óf 7, 70, 700, 7.000, 70.000 of 0.7, 0.007 etc. zijn. Er moet op gelet worden
welke plaats van de eenheden door de gebruiker wordt vastgesteld. Er is een regel, die vaststelt, dat gedurende het
rekenen het onderste van de onderkralen, zowel als de bovenste van de bovenkralen, zo weinig mogelijk gebruikt
moeten worden, omdat het cijfer 5 door een bovenkraal gesteld wordt en het cijfer 10 door de onderkraal van de
volgende rij.